Toward Adaptive Grid Resilience: A Gradient-Free Meta-RL Framework for Critical Load Restoration

Restoring critical loads after extreme events demands adaptive control to maintain distribution-grid resilience, yet uncertainty in renewable generation, limited dispatchable resources, and nonlinear dynamics make effective restoration difficult. Reinforcement learning (RL) can optimize sequential decisions under uncertainty, but standard RL often generalizes poorly and requires extensive retraining for new outage configurations or generation patterns. We propose a meta-guided gradient-free RL (MGF-RL) framework that learns a transferable initialization from historical outage experiences and rapidly adapts to unseen scenarios with minimal task-specific tuning. MGF-RL couples first-order meta-learning with evolutionary strategies, enabling scalable policy search without gradient computation while accommodating nonlinear, constrained distribution-system dynamics. Experiments on IEEE 13-bus and IEEE 123-bus test systems show that MGF-RL outperforms standard RL, MAML-based meta-RL, and model predictive control across reliability, restoration speed, and adaptation efficiency under renewable forecast errors. MGF-RL generalizes to unseen outages and renewable patterns while requiring substantially fewer fine-tuning episodes than conventional RL. We also provide sublinear regret bounds that relate adaptation efficiency to task similarity and environmental variation, supporting the empirical gains and motivating MGF-RL for real-time load restoration in renewable-rich distribution grids.

Learning Neural Networks under Input-Output Specifications

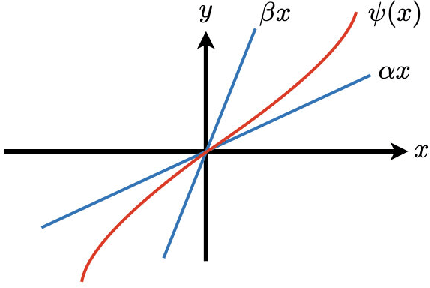
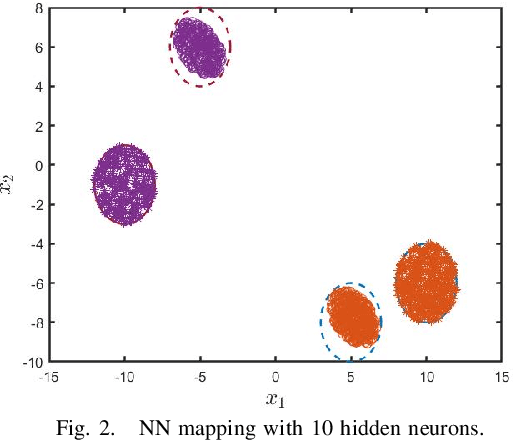
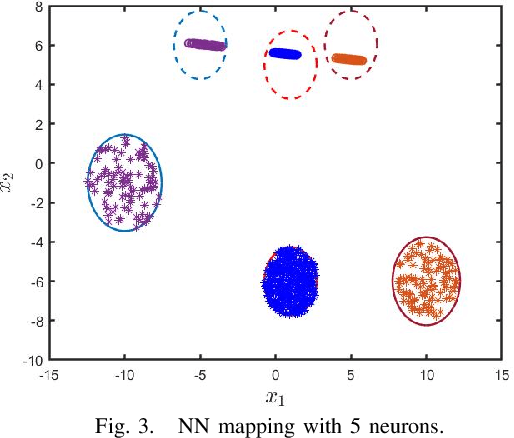
In this paper, we examine an important problem of learning neural networks that certifiably meet certain specifications on input-output behaviors. Our strategy is to find an inner approximation of the set of admissible policy parameters, which is convex in a transformed space. To this end, we address the key technical challenge of convexifying the verification condition for neural networks, which is derived by abstracting the nonlinear specifications and activation functions with quadratic constraints. In particular, we propose a reparametrization scheme of the original neural network based on loop transformation, which leads to a convex condition that can be enforced during learning. This theoretical construction is validated in an experiment that specifies reachable sets for different regions of inputs.